|
Le
AmiPoste-Télécom
accueil
la RégionMont-Saint-Éloi Nord-Pas de Calais les rencontres MICROTEL Le Challenge 2010-2011 éléments de réponse  tranche 1
tranche2
tranche3
tranche 4
tranche 1
tranche2
tranche3
tranche 4
|
Challenge 2010-2011
réponses pour la tranche 2
question 2.1 Le montant de la facture est 7,60 euros ! 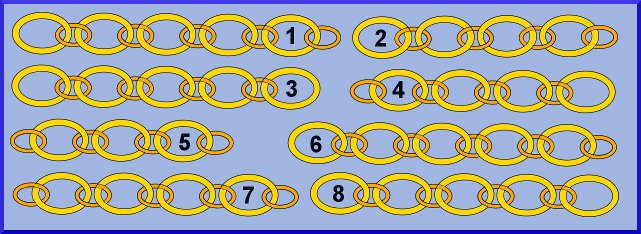
question 2.2
2. Le problème posé par la seconde question est un classique. Nous avons donné un habit neuf à un problème connu comme celui de "la distance de l'horizon", de "la visibilité d'un phare", "de la possibilité de voir le Mont-Blanc depuis la Tour Eiffel" etc. IL y a des dizaines de sites web qui proposent le même calcul. Le problème est lié à la rotondité de la terre, qui définit une zone de vision limitée par l'horizon, manifeste en mer car l'horizon la seule limite au regard. Mais les calculs s'apppliquent sur terre. Notre problème a aussi une connotation historique : les Tours de Mont-Saint-Éloi et le beffroi d'Arras furnet la cible de l'artillerie allemande durant la bataille d'Artois (1915) car elles permettaient aux guetteurs de surveiller la Gohelle et le Douaisis.
La mer est à 80 km de notre village (Berk). Il est donc totalement exclus de voir la mer du haut des Tours. 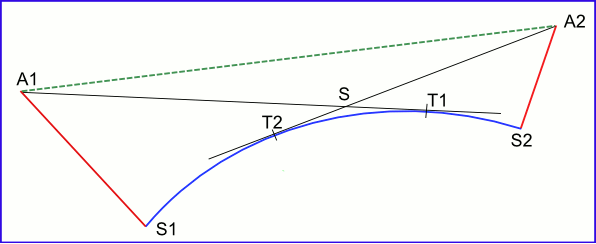
Par contre, Bergues est à 70 km et Amiens à 56 km (en ligne droite). Supposons que S1 soit le lieu des Tours et S2 celui de l'un des deux autres bâtiments. On voit sur le schéma suivant que les limites de vision A1T1 et A2T2 se coupent : de A1 on peut voir A2 (et réciproquement). Il est donc théoriquement possible de voir le haut des deux bâtiments de Bergues et Amiens depuis le haut des Tours. En pratique, c'est vrai pour Amiens ; beaucoup plus limite pour Bergues. Dans notre plat pays, il n'y a pas d'obstacle dont le niveau puisse invalider notre calcul !
question 2.3 1. Le carnaval de Binche attire de plus en plus de visiteurs grâce à sa reconnaissance, en 2003, par l'UNESCO comme faisant partie du patrimoine mondial en tant que chef-d'œuvre du patrimoine oral et immatériel de l'humanité.
3. Le mot "gille" (sans s final) question 2.4
question 2.5 La relative complexité de la partie où il faut conserver la couleur, et qu'il convient de sélectionner, vaut que l'on recherche le "bon outil" de sélection. Expériences faites, deux méthodes se sont révélées intéressantes : * soit on sélectionne au lasso la partie à conserver ; on en fait un calque que l'on fignole à la gomme. * soit utilise un calque temporaire que l'on transforme en sélection ; cette méthode a le mérite d'autoriser les repentirs. L'utilisation de l'adoucissement aide à obtenir une transition "fluide" entre la partie colorée et la partie en niveaux de gris. 
question 2.6 question 2.7 question 2.8
question 2.9
question 2.10
  Second fils de Lazare Carnot mathématicien, physicien (principe de la conservation du travail), homme politique, père également de Sadi, le théoricien de la thermodynamique (le principe de Carnot). Homme politique, Ministre de l'Instruction publique en 1848, il tente de créer une "école de la République", s'avérant un précurseur de Jules Ferry. Père de Sadi (comme son oncle) Carnot, président de la République, assassiné à Lyon en 1894.
question 2.11
1. Chicurium endivia, n'est pas la chicorée endive comme on pourraît le croire. Elle a deux variétés cultivées : la chicorée frisée et la chicorée scarole. 2. Un cultivar de la chicorée endive a été sélectionné pour sa richesse en inuline. L'inuline est un mélanges de sucres de type fructoses que la digestion ne transforme pas monosaccharides, et peut être utilisé par les diabétiques. Elle a par ailleurs de nombreuses applcation en chimie médicale. 3. La barbe de capucin est une salade d'hiver obtenue par la mise en forçage de racines de chicorée sauvage à l'obscurité. Ce forçage provoque la pousse de feuilles étiolées, longues et étroites. Le forçage se faisait en cave et donnait une salade très amère./p>
5.Le nom de "pain de sucre" donné à ce cultivar de chicorée découle de la forme conique qui rappelle celle d'un pain de sucre. Cette plante développe des feuilles très amples, oblongues avec de grosses nervures qui s'enroulent, serrées les unes contre les autres pour former une pomme allongée vert clair. C'est une salade d’hiver croquante qui résiste au froid. Elle se consomme crue en salade ou cuite en gratin, au jus, à la béchamel. question 2.12 1. Le 21 novembre 1806 le Décret de Berlin instaure le Blocus continental. Le but est de ruiner le commerce maritime de l'Angleterre. Une importante recherche agro-alimentaire se développe pour remplacer les produits coloniaux : le sucre est désormais issu de la betterave, et la chicorée est un succédané du café. 2. La chicorée endive est nommé en néerlandais witlof qui devient en flamand occidental witloof, mot utilisé dans toute la Belgique. Ce mot signifie feuillage (lof) blanc (wit) 3. Un chercheur belge du nom de Parmentier eut l'idée dès le début des années 50 de forcer les endives dans des salles climatisées. 4. Le savoir-faire des endiviers du Nord de la France groupés au sein du CELFNORD (Comité Economique Agricole des Légumes et Fruits du Nord de la France) les a amenés en 1983 à produire une endive baptisée « la Perle du Nord ». 
5. Un forçage hors sol demande 3 à 4 semaines. Le forçage en pleine terre (cf.photo) demande 10 à 16 semaines. Le prix en est doublé, voire triplé selon la période.
question 2.13 1. Le Conseil Général du Nord a fait construire la Villa Marguerite Yourcenar pour abriter le Centre Départemental de Résidence d'Ecrivains Européens qui a pour mission d'accueillir des écrivains qui trouvent là un lieu retiré et paisible pour écrire, mais aussi de faire découvrir leur œuvre au grand public en organisant diverses manifestations. 2. la carte 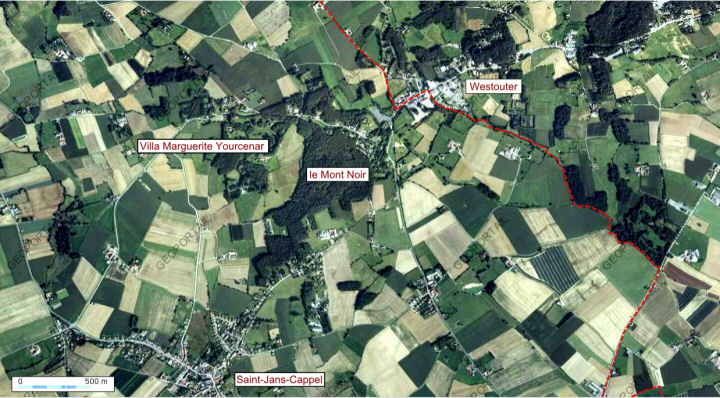 3. Michel-Charles Cleenewerck de Crayencour était vice-président du conseil de préfecture. Son hôtel était au 25 rue Marais à Lille, aujourd'hui 25 rue Jean Moulin. 3. Michel-Charles Cleenewerck de Crayencour était vice-président du conseil de préfecture. Son hôtel était au 25 rue Marais à Lille, aujourd'hui 25 rue Jean Moulin.
question 2.14
Au départ, il y a une exercice de l'atelier "tableur" : l'idée est de réaliser la table de Pythagore de façon simple, en privilégiant le couper/coller et en limitant les saisies directes de valeurs.
Voici une solution répondant à ces contraintes :
Pour les forts en thèmes, voici une solution minimale, qui oblige à créer une grosse formule et relève plus de l'esprit "macro"...
question 2.15 Il convient de décomposer les informations en octets et même en quartets. Puis de transformer chaque quartet en écriture hexadécimale, plus maniable : ligne 1 : 4C 27 C3 A9 ligne 2 : 74 65 72 6E ligne 3 : 69 74 C3 A9 ligne 4 : 20 70 65 75 ligne 5 : 74 2D C3 AA ligne 6 : 74 72 65 3F ligne 7 : 25 07 20 10 1. La date de ce dimanche apparaît en clair en ligne 7 si c'est du BCD : 25 juillet 2010. 2. Le nombre de Maïa est : 0x4C27C3A97465726E6974C3A920706575742DC3AA7472653F
Pour trouver le nombre de chiffres de la valeur décimale, il existe diverses techniques : 1867323241393798996504717134445207048059432600673128179007 1 867 323 241 393 798 996 504 717 134 445 207 048 059 432 600 673 128 179 007 *** soit on recherche combien de chiffres décimaux donnent les 46 chiffres hex qui suivent le 0x4C, qui lui, vaut 76 en décimal : il faut évaluer 76 x 16^46. Une simple calculette donne : 1.8635...exp57.
*** soit on se dit que 2^10 ~ 10^3 ; il y a 192 binaires soit 2+190. Les deux premiers binaires sont 0 et 1. Une approximation du nombre de Maïa est donc 1 x 2^190 ou (par défaut) 10^(19 x 3) soit 10^57, nombre de 58 chiffres.
3. Il n'y a en pratique quotidienne que deux codages de textes utilisés dans nos pays : le codage latin-1 (avec des variantes mineures) et l'Unicode. L'Unicode apparaît dans nos mail ou nos textes sous sa forme UTF-8. Il suffit de taper le codage de Maïa dans un éditeur (PSPAD, GEANY, NOTEPAD++) et de lire soit en latin-1, soit en UTF-8. On peut faire de même avec une page html. 4C 27 C3 A9 74 65 72 6E 69 74 C3 A9 20 70 65 75 74 2D C3 AA 74 72 65 3F L ' à © t e r n i t à © p e u t - à ª t r e ? Cette traduction fait penser à de l'UTF-8. En effet, les caractère accentués sont explicités sur deux octets ; C3 A9 est le é, C3 AA le ê. Le titre du manga :
question joker Cette question reprend avec le même intitulé celle posé dans le Challenge de Poussay en 2006. Dans le problème de Poussay, il y avait deux chances sur trois de voir Ludovic (p=2/3) et, s'il venait, une chance sur deux (r=1/2) qu'il soit à l'heure. Modélisons la situation pour éviter les considérations théoriques, mais avec les valeurs p=3/5 et r=1/3 et supposons qu'il y ait deux réunions par semaine. Sur un an, cela devrait faire n=105 réunions.
La répartition espérée est la suivante : 
1. Dans l'hypothèse où la probabilité de voir arriver Ludovic est de 1/2, on voit que les cas d'absence ou de retard doivent ête égaux : (1-p).n = p.n.(1-r) soit encore 1-p = p.(1-r) ou enfin p(2 - r) = 1. Le problème est donc de trouver des fractions pour p et r de façon que le résultat soit 1/2. On a p(2 - r) = 1. Le choix est fort restreint : le dénominateur est 2, 3, 4 ou 5. Le numérateur est strictement inférieur au dénominateur. La fraction doit être irréductible. Et comme (2-r) est compris entre 1 et 2, p est supérieur à 1/2.
*** Le numérateur de p ne peut être 1 et 2/5 ne convient pas.
2. Voici un script de simulation en Python.
from random import uniform, seed
venir = 3/4
ok = 2/3
retard = 1 - ok
def atelier () :
v = uniform (0, 1.0)
r = uniform (0, 1.0)
if v > venir :
return -1 # Ludovic ne vient pas
if r > ok :
return 0 # Ludovic est à l'heure
else :
return 1 # Ludovic est en retard
def epreuve () :
absent = 0
apres_heure = 0
heure_ok = 0
for i in range(1000) : # mille essais
r = atelier ()
if r == 1 :
heure_ok += 1
elif r == 0 :
apres_heure += 1 # Ludovic est en retard
else :
absent += 1 # Ludovic est absent
print ('A=',absent,'ok=',heure_ok, 'R=', apres_heure,"\n",\
apres_heure/(apres_heure+absent))
for test in range(20) :
epreuve()
et les quatre résultats non triviaux obtenus :
|
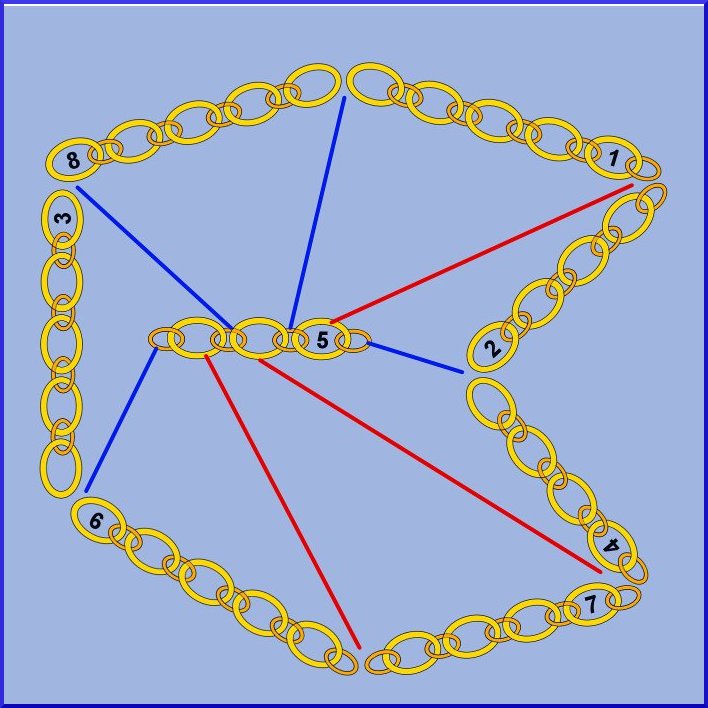
 le collier de Dagobert
le collier de Dagobert 1. Les beffrois de la région sont surmontés d'une girouette. Celui d'Arras est un lion (Le Lion d'Or, portant un soleil pour évoquer le rattachement çà la France par Louis XIV), comme celui de Bergues qui familièrement se voit affubler du surnom de "Nicolas". Voici sa photo, à gauche.
1. Les beffrois de la région sont surmontés d'une girouette. Celui d'Arras est un lion (Le Lion d'Or, portant un soleil pour évoquer le rattachement çà la France par Louis XIV), comme celui de Bergues qui familièrement se voit affubler du surnom de "Nicolas". Voici sa photo, à gauche.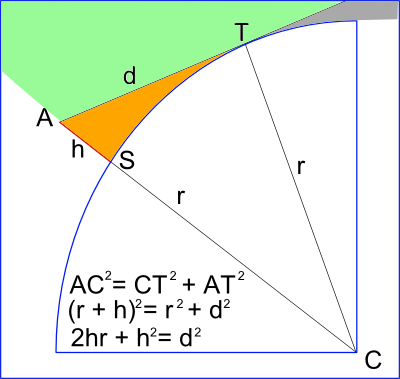 Le schéma de droite montre comment calculer, depuis un point d'observation à l'altitude h=AS la distance de l'horizon AT, connaissant le rayon de la terre r. Pour des raisons de clarté, les échelles sont très exagérées : h (de l'ordre de 100 m) est très faible par rappport à r (plus de 6000 km). La distance AT est également faible par rapport à r qinsi que la distance au sol ST. AT et ST peuvent être confondues.
Le schéma de droite montre comment calculer, depuis un point d'observation à l'altitude h=AS la distance de l'horizon AT, connaissant le rayon de la terre r. Pour des raisons de clarté, les échelles sont très exagérées : h (de l'ordre de 100 m) est très faible par rappport à r (plus de 6000 km). La distance AT est également faible par rapport à r qinsi que la distance au sol ST. AT et ST peuvent être confondues. 2. Une trouille est en patois un personnage malpropre, une "truie". Le mot "nouille" est vraisemblablement un dérivé de "guenouille" (en patois, guenille). Les trouilles de nouilles sont des personnage grossièrement travestis et masqués qui, le lundi précédant les jours gras, envahissent les rues de Binches. Ces masques prennent un malin plaisir à intriguer les personnes non masquées. Ils montrant à leurs victimes qu'ils les connaissent en révélant des choses parfois intimes. La victime qui ne reconnait pas son tourmenteur lui paie un verre qu'il boit avec une paille pour ne pas relever le masque.
2. Une trouille est en patois un personnage malpropre, une "truie". Le mot "nouille" est vraisemblablement un dérivé de "guenouille" (en patois, guenille). Les trouilles de nouilles sont des personnage grossièrement travestis et masqués qui, le lundi précédant les jours gras, envahissent les rues de Binches. Ces masques prennent un malin plaisir à intriguer les personnes non masquées. Ils montrant à leurs victimes qu'ils les connaissent en révélant des choses parfois intimes. La victime qui ne reconnait pas son tourmenteur lui paie un verre qu'il boit avec une paille pour ne pas relever le masque. 1. Joseph-Bienaimé Caventou est né à Saint Omer, le 30 juin 1795 et est mort le 5 mai 1877. En 1819, Caventou fait la connaissance de Joseph Pelletier, professeur adjoint à l'Ecole de Pharmacie de Paris. De cette collaboration avec Pelletier vont surgir d'importants travaux dont la découverte de la quinine (1820). Un cratère de 3 km sur la lune porte le nom de Caventou.
1. Joseph-Bienaimé Caventou est né à Saint Omer, le 30 juin 1795 et est mort le 5 mai 1877. En 1819, Caventou fait la connaissance de Joseph Pelletier, professeur adjoint à l'Ecole de Pharmacie de Paris. De cette collaboration avec Pelletier vont surgir d'importants travaux dont la découverte de la quinine (1820). Un cratère de 3 km sur la lune porte le nom de Caventou. 3. Joseph Liouville (24 mars 1809 à Saint-Omer - 8 septembre 1882 à Paris) est un mathématicien français.
3. Joseph Liouville (24 mars 1809 à Saint-Omer - 8 septembre 1882 à Paris) est un mathématicien français.  4. Pierre-Alexandre Monsigny est un compositeur français né à Fauquembergues (Pas-de-Calais) le 17 octobre 1729 et mort à Paris le 14 janvier 1817.
4. Pierre-Alexandre Monsigny est un compositeur français né à Fauquembergues (Pas-de-Calais) le 17 octobre 1729 et mort à Paris le 14 janvier 1817.
 Il se révèle comme le principal précurseur, d'un genre nouveau : l'opéra-comique. Il ouvre ainsi la voie à Boïeldieu, Auber, Gounod, Bizet, Massenet… à tous ceux qui, par leur talent de compositeur, sont parvenus à illustrer avec succès ce genre bien français.
Il se révèle comme le principal précurseur, d'un genre nouveau : l'opéra-comique. Il ouvre ainsi la voie à Boïeldieu, Auber, Gounod, Bizet, Massenet… à tous ceux qui, par leur talent de compositeur, sont parvenus à illustrer avec succès ce genre bien français.
 4. La chicorée rouge n'est rouge que si on la cueille après les premiers froids. On cultive la chicorée rouge de Véronne et la chicorée rouge de Trévise. C'est une chicorée qui donne de petites pommes et que l'on récolte en hiver.
4. La chicorée rouge n'est rouge que si on la cueille après les premiers froids. On cultive la chicorée rouge de Véronne et la chicorée rouge de Trévise. C'est une chicorée qui donne de petites pommes et que l'on récolte en hiver.